For those who had to decide on a couple of phrases or symbols to encapsulate your legacy, what would you choose? Johann Carl Friedrich Gauss (1777–1855) left behind a trophy case stocked with mathematical achievements to select from, however above all, he wished a “common heptadecagon” etched on his gravestone. The extremely symmetrical 17-sided form starred in a proof that Gauss thought of one in all his biggest contributions to math. At simply 18 years outdated Gauss used a heptadecagon to unravel a traditional downside that had stumped mathematicians for greater than 2,000 years. A tour by means of that historical past reveals deep connections between the traditional conception of shapes as drawings and a contemporary perspective of the equations that govern them.
Historical Greek Geometry
The traditional Greeks excelled at geometry, inserting particular emphasis on constructions created with a compass and straightedge. Consider these constructions as diagrams with desired geometric properties created solely with a writing utensil and two instruments. Given two factors, a compass (to not be confused with the navigational machine) attracts a circle centered at both level that passes by means of the opposite level. A straightedge attracts straight traces between the factors. Neither instrument has any markings on it, so they can’t measure distances or angles.
On supporting science journalism
For those who’re having fun with this text, think about supporting our award-winning journalism by subscribing. By buying a subscription you might be serving to to make sure the way forward for impactful tales concerning the discoveries and concepts shaping our world as we speak.
The Greeks didn’t impose arbitrary guidelines simply to make math tougher. The sport of developing shapes with a compass and straightedge originates in Euclid’s Parts, one of the crucial essential textbooks ever written. Like fashionable mathematicians, Euclid got down to derive all of geometry from a minimal record of assumptions known as postulates. As an alternative of merely asserting the existence of shapes or different geometric objects, Euclid wished to construct them explicitly from the only substances: traces and circles.
To get a really feel for these constructions, attempt one for your self. Given the road section from A to B beneath, discover its midpoint. Eyeballing received’t suffice; your methodology should discover the precise midpoint.
First use the compass to attract a circle centered at A and passing by means of B (first panel). Then repeat this step with the circle centered at B and passing by means of A (second panel). These circles intersect at two factors. Use the straightedge to attach these factors (third panel). By the symmetry in our building, this vertical line will intersect the unique line section precisely at its midpoint.
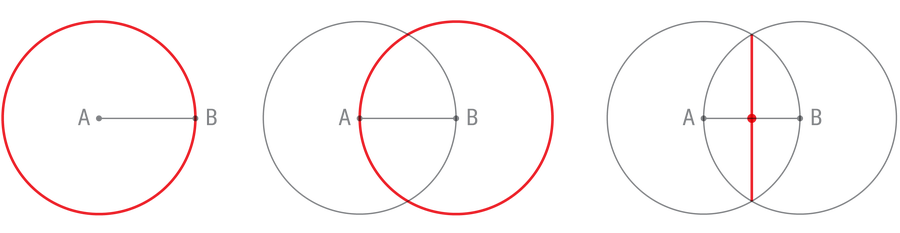
This building does way more than bisect a line section. It creates a proper angle between the 2 traces, which isn’t a trivial feat with such a restricted instrument set. And by connecting a couple of extra factors, you can also make an equilateral triangle—one whose sides have equal lengths (and whose angles have equal measure).
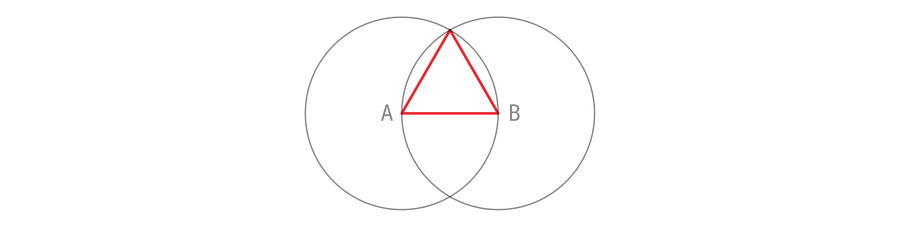
Discover that every fringe of the triangle can also be a radius of one of many circles. The circles are the identical measurement and due to this fact all of the triangle’s sides have the identical size. So equilateral triangles are constructible with a compass and straightedge, QED. Congratulations on persisting by means of the first proposition within the first guide of Euclid’s Parts. Solely 13 extra books to go.
A Roadblock
Of all of the shapes that one can assemble with a compass and straightedge, common polygons maintain a particular cachet. Polygons are enclosed shapes composed of straight-line edges, equivalent to triangles and rectangles (versus curved shapes equivalent to circles or unenclosed shapes such because the letter E). Common polygons have essentially the most symmetry in that their sides all have equal size and their angles all have equal measure (like squares and equilateral triangles however in contrast to rectangles and rhombuses). Developing any outdated irregular triangle with a compass and straightedge is baby’s play—simply scatter three factors on the web page and join them with traces. However developing our completely symmetric equilateral triangle—an everyday polygon—required some elegant legwork.
Euclid discovered the way to assemble common polygons with three, 4 and 5 sides—or equilateral triangles, squares and common pentagons, respectively. He squeezed a couple of extra generalizations out of those core constructions; as an illustration, after you have an everyday polygon on the web page, a easy maneuver will produce a brand new common polygon with double the variety of sides.
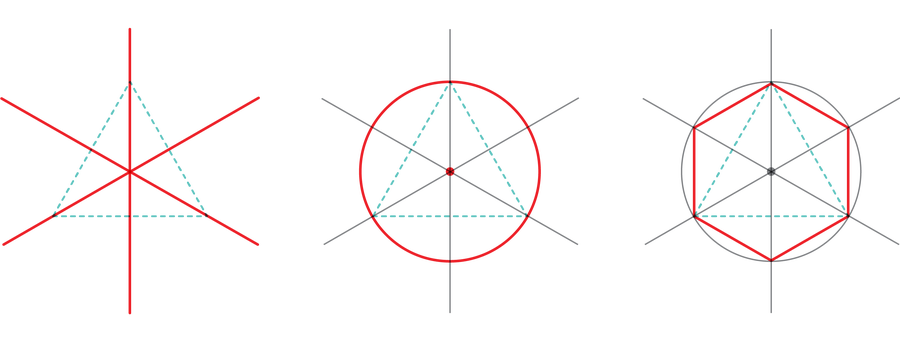
You possibly can repeat this doubling process as many occasions as you would like. Meaning three-, four- and five-sided common polygons will be reworked into six-, eight- and 10-sided common polygons, in addition to 12-, 16- and 20-sided ones, and so forth. Euclid additionally confirmed the way to “multiply” the three- and five-sided common polygons to provide a common 15-gon.
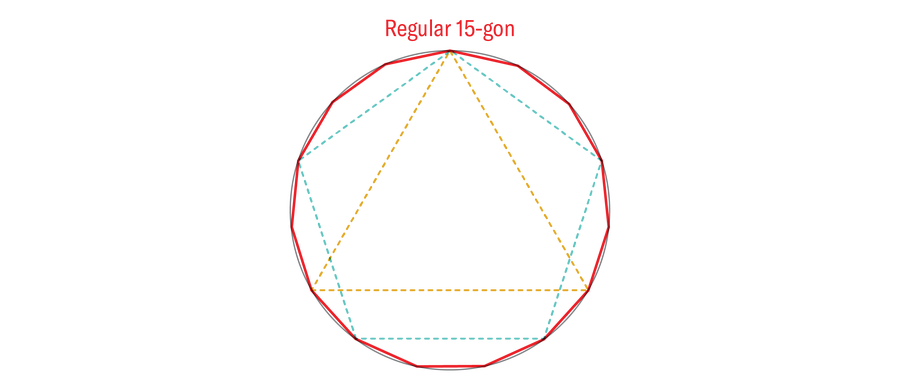
Progress halted there. By some means Euclid knew {that a} common 3,072-gon was constructible in precept (a triangle doubled 10 occasions), however he had no concept the way to assemble an everyday seven-gon (heptagon) or 11-gon (hendecagon). To be clear, common polygons of any variety of sides higher than two do exist and will be constructed with extra succesful instruments. The query that Euclid left behind asks which of them are constructible with a compass and straightedge alone. This query would stay unanswered for 2 millennia till a sure German teenager picked up a pencil.
18th-Century Math to the Rescue
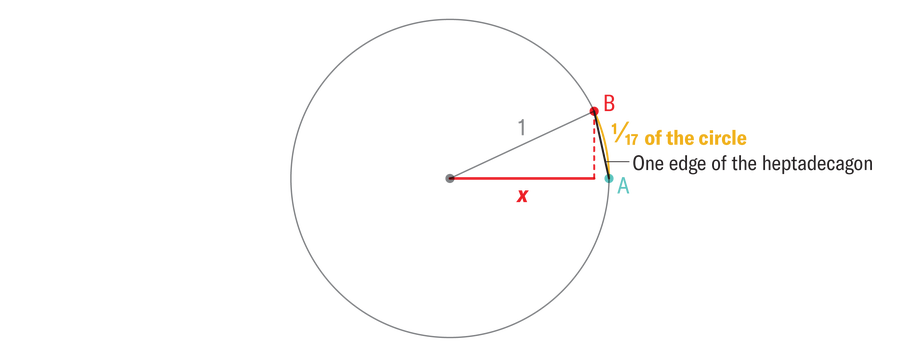
By 1796 no new common polygons had joined the pantheon of constructible shapes, but mathematicians had acquired a deeper understanding of compass and straightedge constructions. Gauss knew the way to scale back the issue of developing an everyday polygon to that of merely developing a line section with a really particular size. To see the way to create a 17-gon, begin with a unit circle (the place the radius equals one) and some extent A on the circle. Think about we might discover the crimson level B above A precisely one seventeenth of the best way across the circle. If we might assemble the crimson level from the blue level, we might repeat that building all the best way across the circle, join the dots with our straightedge, and voilà, an everyday heptadecagon. How can we draw level B, given level A, although? Discover that if we might draw the crimson line section labeled x, then we will hint that as much as the crimson level B, and we win. The complete downside of developing an everyday heptadecagon boils all the way down to developing a line section with the exact size x. For the mathematically curious, x = cosine (2π ⁄17).
Can a compass and straightedge assemble a line section of any size? By Gauss’s time, mathematicians knew the stunning reply to this query. A size is constructible precisely when it may be expressed with the operations of addition, subtraction, multiplication, division or sq. roots utilized to integers. So some unusual numbers such because the sq. root of 99⁄5 are constructible (99 and 5 are integers, and we’ve utilized division and sq. root to them), whereas some extra acquainted numbers equivalent to pi (π) and the dice root of two can’t be constructed as a result of one can by no means write them when it comes to these 5 operations alone.
Remarkably, the rudimentary instruments that the traditional Greeks used to attract their geometric diagrams completely match the pure operations of modern-day algebra: addition (+), subtraction (–), multiplication (x), division (/) and taking sq. roots (√). The rationale stems from the truth that the equations for traces and circles solely use these 5 operations, a perspective that Euclid couldn’t have envisioned within the prealgebra age.
It’d shock you to be taught that Gauss by no means truly drew an everyday heptadecagon. He didn’t have to. He proved that the form is constructible in precept by expressing the particular size x [cosine (2π ⁄17)] solely when it comes to the 5 algebraic operations that the compass and straightedge allow. Even in case you don’t discover his equation significantly enlightening, its complexity demonstrates how a lot work the adolescent will need to have poured into the issue:

Much more spectacular, Gauss absolutely characterised which common polygons are constructible and which aren’t (though it was not till 1837 that Pierre Wantzel offered a rigorous proof that Gauss’s characterization didn’t pass over something). So not solely did Gauss describe the shape that each one constructible common polygons take, he and Wantzel vindicated Euclid’s frustrations by proving that the elusive common heptagon (seven sides) and hendecagon (11 sides) are unattainable to assemble with a compass and straightedge alone, together with infinitely many different shapes.
In response to biographer G. Waldo Dunnington, Gauss felt nice satisfaction in cracking the millennia-old downside and advised a good friend that he wished an everyday heptadecagon displayed on his gravestone. Sadly, this didn’t occur, however a monument in Gauss’s delivery metropolis of Brunswick, Germany, boasts a 17-pointed star engraved on the again. The stonemason selected a star as a result of he believed that individuals couldn’t distinguish a heptadecagon from a circle. I’m wondering if Euclid would agree.





